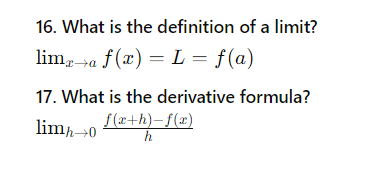What is the formula for slope?

1. What is the formula for slope?
y2−y1x2−x1\frac{y_2 – y_1}{x_2 – x_1}

2. What is the equation of a line?
y=mx+by = mx + b

3. What is a quadratic function?
ax2+bx+cax^2 + bx + c

4. What is the quadratic formula?
x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}

5. What is the interval where the solution exists?
(−∞,−6)∪(9,∞)(-\infty, -6) \cup (9, \infty)

6. What is the solution for all real numbers between -6 and 9?
(−6,9)(-6, 9)

7. What does break-even mean in economics?
Cost = Revenue or Profit = 0

8. What is the revenue function?
Price * Number of Units

9. What is the profit function?
Revenue – Cost

10. What is the cost function?
Variable Cost * Number of Units + Fixed Cost

---

Suppose a company has fixed cost of $45 and variable cost per unit of 17x+917x + 9 dollars, where xx is the total number of units produced. Suppose further that the selling price of its product is 18−67×18 – 67x dollars per unit.

---

11. Find the simplified cost function, C(x)C(x).

• a. $45
• b. 17×2+9x17x^2 + 9x
• c. 17×2+9x+4517x^2 + 9x + 45
• d. 17×2+54x17x^2 + 54x
• e. None of these
  Answer: c. 17×2+9x+4517x^2 + 9x + 45

12. Find the simplified revenue function, R(x)R(x).

• a. 18x−67x218x – 67x^2
• b. 18x−67×2−4518x – 67x^2 – 45
• c. 18x−67x18x – 67x
• d. $45
• e. None of these
  Answer: a. 18x−67x218x – 67x^2

13. Find the simplified profit function, P(x)P(x).

• a. x2−9x−45x^2 – 9x – 45
• b. −x2+9x−45-x^2 + 9x – 45
• c. −17×2+9x-17x^2 + 9x
• d. $0
• e. None of these
  Answer: b. −x2+9x−45-x^2 + 9x – 45

---

14. What is the relationship between marginal revenue and the slope of the revenue function?

• a. There is no relationship.
• b. Marginal revenue is the negative reciprocal of the slope.
• c. They are the same.
  Answer: c. They are the same.

15. What does it mean for a function to be differentiable at a point?

• a. The limit as xx approaches the point does not exist.
• b. The function is not continuous at the point but is differentiable at the point.
• c. The function is continuous and differentiable at that point.
• d. The function is continuous at the point but is not differentiable at the point.
• e. None of these.
  Answer: c. The function is continuous and differentiable at that point.

16. What is the definition of a limit?
lim⁡x→af(x)=L=f(a)\lim_{x \to a} f(x) = L = f(a)

17. What is the derivative formula?
lim⁡h→0f(x+h)−f(x)h\lim_{h \to 0} \frac{f(x + h) – f(x)}{h}